O triângulo equilátero é uma figura geométrica fascinante que aparece em diversas situações no nosso dia a dia, sendo fundamental em vários campos da matemática e até em design e arquitetura. Nesse sentido, neste post, vamos explorar a definição, as propriedades desse triângulo, como calcular sua área e ainda algumas de suas aplicações práticas.
O Que é um Triângulo Equilátero?
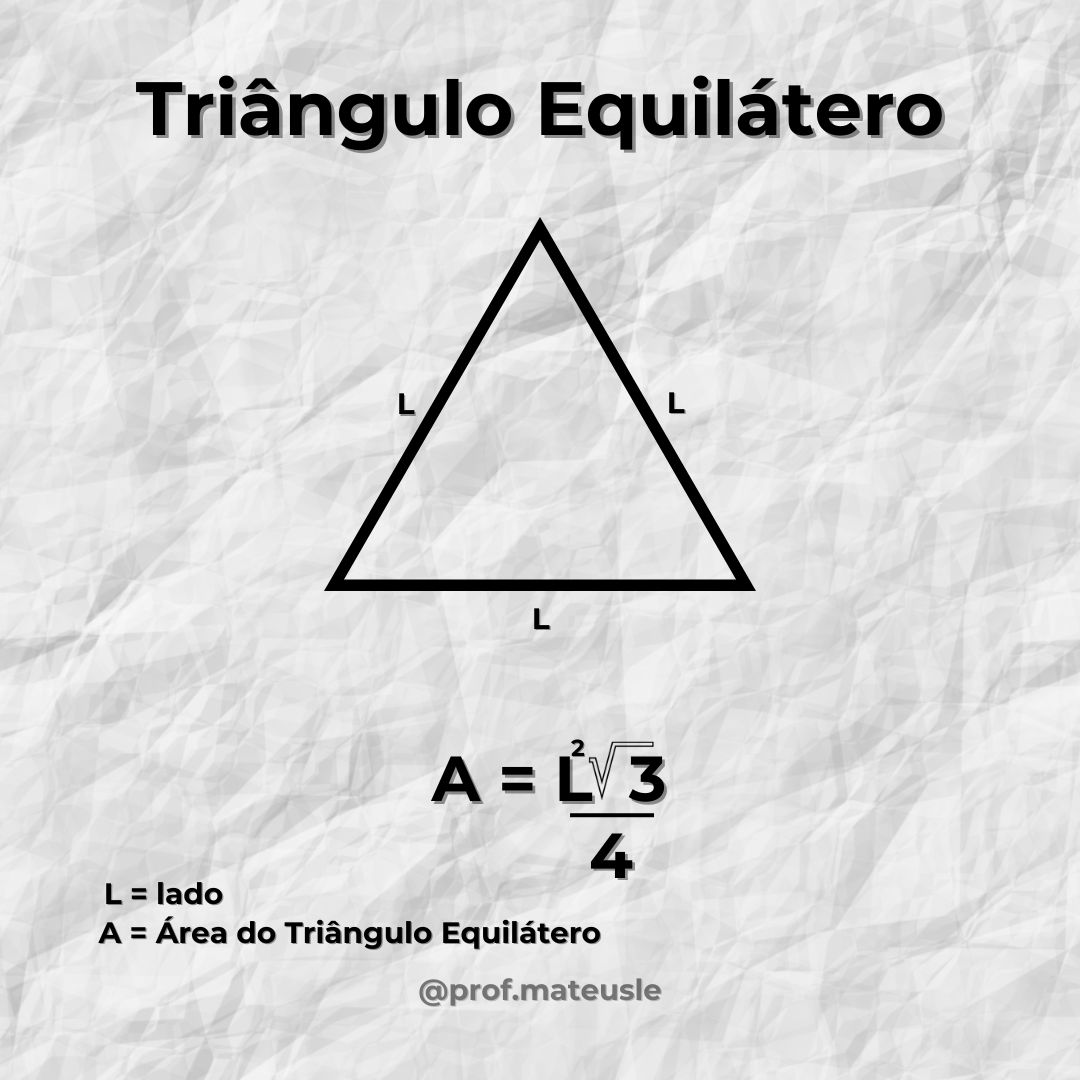
Primordialmente, um triângulo equilátero é um tipo específico de triângulo onde todos os três lados têm o mesmo comprimento, e todos os três ângulos internos são iguais, medindo 60° cada. Ou seja, um triângulo equilátero é simétrico tanto em termos de lados quanto de ângulos.
Definição
- Lados: Todos os três lados são congruentes (iguais em comprimento).
- Ângulos: Todos os ângulos internos possuem 60°.
Esse tipo de triângulo é considerado uma das formas mais simples e perfeitas na geometria, e suas propriedades tornam-no muito útil em diversas áreas do conhecimento.
Propriedades do Triângulo Equilátero
O triângulo equilátero possui diversas propriedades interessantes que o tornam único:
- Simetria:
O triângulo equilátero tem três eixos de simetria. Isso significa que ele pode ser dobrado ao meio de três maneiras diferentes, e em todas as situações, as duas metades serão idênticas. - Perímetro:
O perímetro de um triângulo equilátero é simplesmente a soma dos três lados. Como todos os lados são iguais, o cálculo é bem simples: P=3×lado - Área:
A área de um triângulo equilátero pode ser calculada utilizando a fórmula:
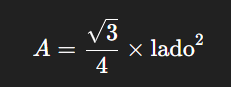
Onde “lado” representa o comprimento de qualquer um dos lados do triângulo. A fórmula é derivada a partir de conceitos de trigonometria e geometria básica.
4. Altura:
Calcula-se a altura do triângulo equilátero utilizando a fórmula:
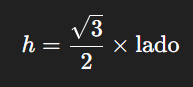
A altura é a distância perpendicular entre qualquer vértice e o meio do lado oposto.
5. Centroides e Circuncentro:
Além disso, no triângulo equilátero, o centro de massa (ou centroide), o ponto de interseção das medianas, e o circuncentro (centro da circunferência que passa por todos os vértices) coincidem. Ou seja, todos esses pontos estão no mesmo local, no centro do triângulo.
Como Calcular a Área do Triângulo Equilátero?
Calcular a área de um triângulo equilátero é uma tarefa simples, desde que você conheça o comprimento de um de seus lados. Vamos mostrar um exemplo para entender melhor a aplicação da fórmula.
Exemplo:
Suponha que o lado do triângulo equilátero tenha 6 cm. Para calcular a área, basta aplicar a fórmula:
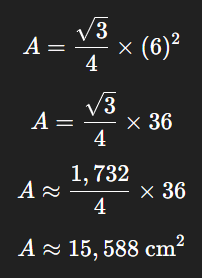
Portanto, a área do triângulo equilátero é aproximadamente 15,59 cm².
Utilização do Triângulo Equilátero no Dia a Dia
Embora o triângulo equilátero seja um conceito matemático, ele aparece com bastante frequência em várias situações cotidianas e em diversas áreas do conhecimento:
- Arquitetura e Design:
Usado no design de estruturas geométricas, pois sua simetria oferece estabilidade e equilíbrio. Além disso, ele aparece em muitos padrões de piso, telhados e outros elementos arquitetônicos. - Engenharia e Física:
No estudo de tensões e forças, usamos para representar sistemas de forças equilibradas. Sua simetria facilita a análise desses sistemas. - Arte e Decoração:
Em diversas formas de arte utilizado para criar padrões simétricos. Ele também é uma figura comum em mandalas e outras representações artísticas. - Jogos e Brinquedos:
Frequentemente encontrado em peças de quebra-cabeça, como o tangram, e em brinquedos de construção, como as peças que formam modelos geométricos.
Conclusão
Enfim, o triângulo equilátero é uma figura fundamental na geometria, com propriedades matemáticas interessantes e diversas aplicações práticas. Logo, seu formato perfeito e simétrico o torna uma ferramenta importante em várias áreas, desde a arquitetura até a física e a arte. Sendo assim, com uma fórmula simples para calcular sua área e várias características únicas, o triângulo equilátero é um exemplo claro de como a matemática se relaciona diretamente com o nosso cotidiano.
Em síntese, se você está começando a estudar geometria ou se já é um entusiasta da matemática, entender as propriedades do triângulo equilátero é uma excelente maneira de reforçar seus conhecimentos.