O triângulo é uma das figuras geométricas mais fundamentais e essenciais na matemática. Desse modo, com suas três linhas e três vértices, o triângulo é a base de muitos conceitos geométricos e aparece frequentemente em diversas áreas da ciência, engenharia, arquitetura e até mesmo na natureza. Então, neste post, vamos explorar o que torna o triângulo uma figura tão importante, suas propriedades fundamentais, tipos e aplicações práticas.
O Que é um Triângulo?
Um triângulo é uma figura geométrica composta por três lados e três vértices, formando três ângulos internos. A simplicidade de sua estrutura torna o triângulo a figura geométrica mais simples, mas, ao mesmo tempo, uma das mais poderosas. Desta forma, ele pode classificar de várias maneiras, dependendo de suas características, como o comprimento dos lados ou a medida de seus ângulos.
Tipos de Triângulos
Existem diversas classificações para os triângulos, com base em suas propriedades. As principais são:
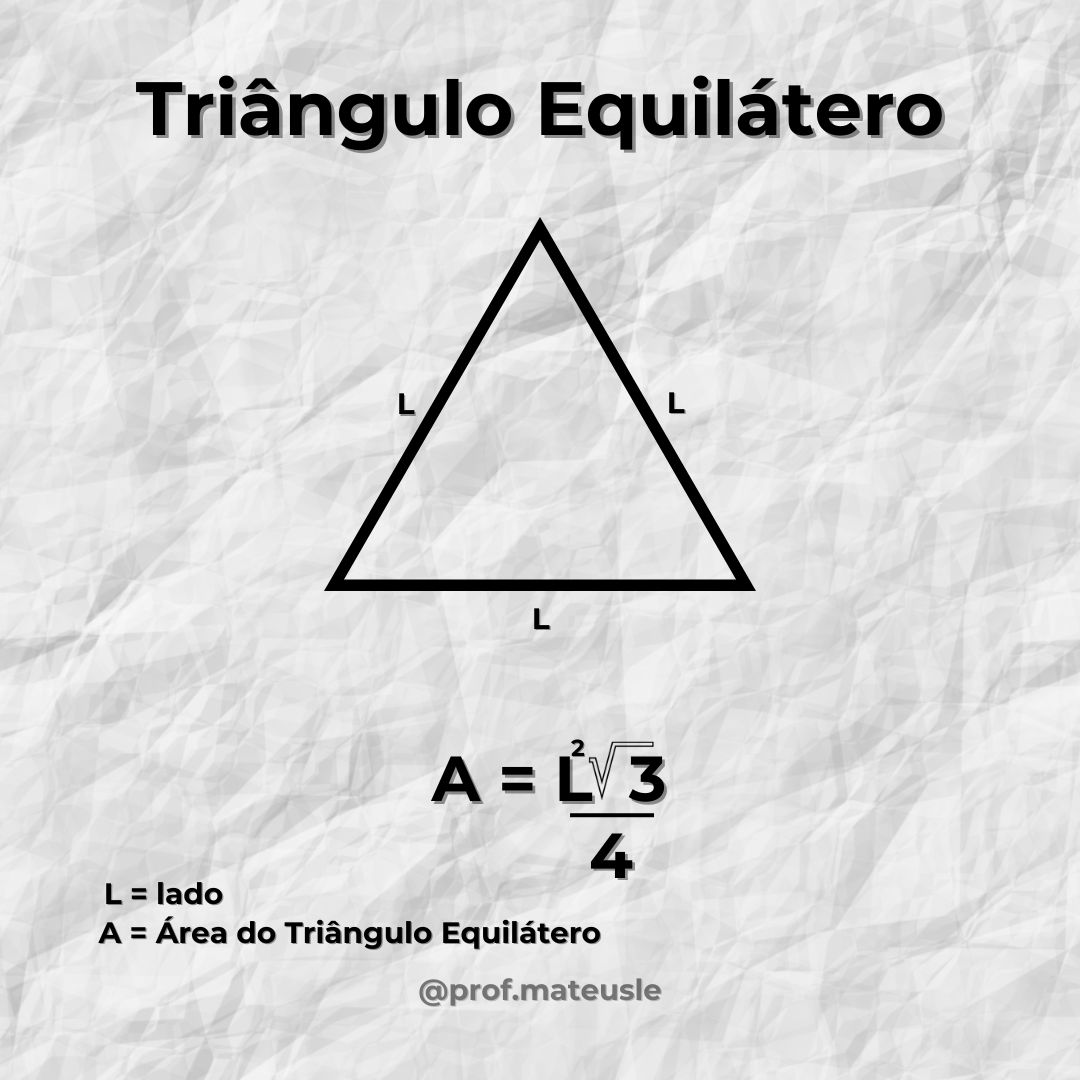
- Triângulo Equilátero: Todos os três lados têm o mesmo comprimento, e todos os ângulos internos medem 60 graus. É um caso especial de triângulo que possui simetria total.
- Triângulo Isósceles: Possui dois lados de igual comprimento e dois ângulos internos de mesma medida. A base é o lado diferente, e a simetria se dá em relação à altura que divide a base ao meio.
- Triângulo Escaleno: Seus três lados têm comprimentos diferentes, e os ângulos internos também são distintos. Esse tipo de triângulo não possui simetria.
- Triângulo Acutângulo: Todos os ângulos internos são menores que 90 graus.
- Triângulo Retângulo: Um dos ângulos internos é exatamente 90 graus. Esse tipo de triângulo é fundamental em muitas áreas da matemática, especialmente na trigonometria.
- Triângulo Obtusângulo: Um dos ângulos internos é maior que 90 graus.
Propriedades Importantes do Triângulo
Por isso que os triângulos possuem várias propriedades essenciais que ajudam a entender a geometria de forma mais profunda. Assim, aqui estão algumas das principais:
- Soma dos Ângulos Internos: A soma dos ângulos internos de qualquer triângulo é sempre igual a 180 graus.
- Desigualdade Triangular: A soma de qualquer dois lados de um triângulo sempre será maior que o comprimento do terceiro lado. Isso é essencial para a construção de triângulos na prática.
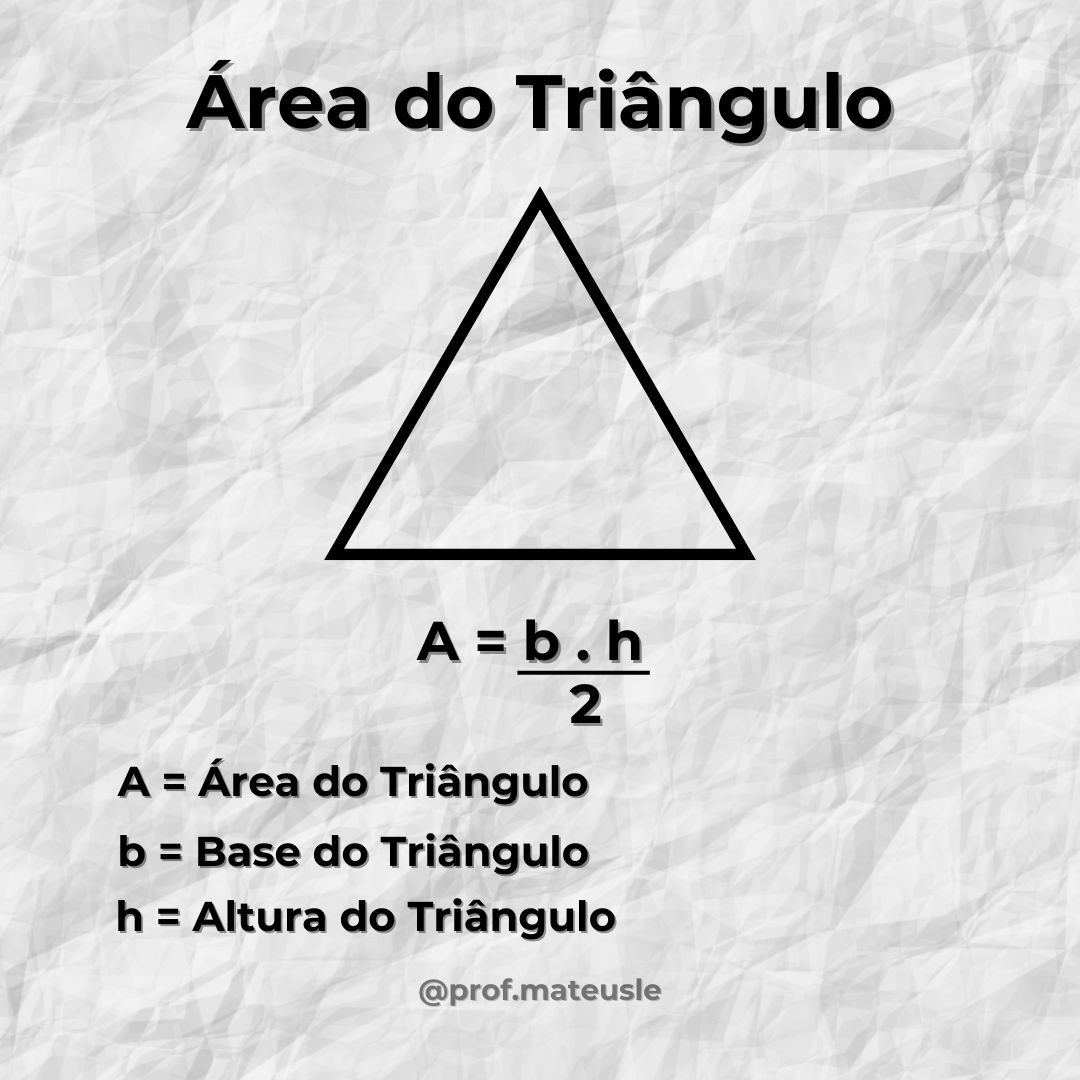
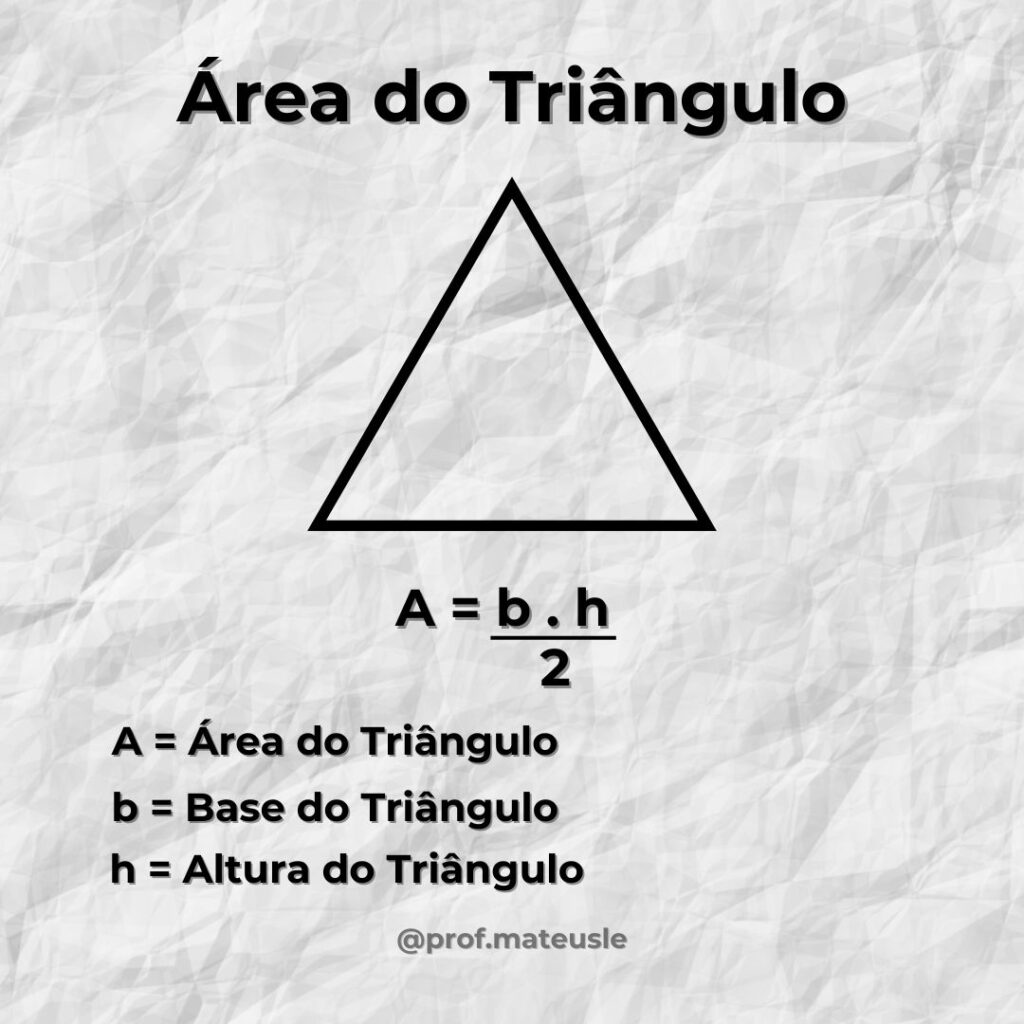
- Área do Triângulo: A fórmula básica para calcular a área de um triângulo é:
Aplicações do Triângulo no Mundo Real
Em seguida, os triângulos são uma das formas geométricas mais versáteis e essenciais, com uma ampla gama de aplicações no mundo real. Portanto, aqui estão algumas das principais áreas em que utilizam os triângulos:
1. Arquitetura e Engenharia
Ainda por cima, em projetos arquitetônicos e de engenharia, especialmente devido à sua estabilidade e resistência usam os triângulos. A estrutura triangular é fundamental em pontes, telhados e vigas. Isso ocorre porque, quando submetido a pressão, de maneira eficiente pelo triângulo o peso distribui, evitando deformações.
2. Navegação e Cartografia
Na navegação e na cartografia, em técnicas de triangulação para determinar distâncias e localizações geográficas usam os triângulos. Por exemplo, os sistemas de GPS utilizam a triangulação entre satélites e receptores para calcular a posição exata em um mapa.
3. Design e Arte
Além do mais, no design gráfico e na arte, como elementos estéticos poderosos usam os triângulos. Eles ajudam a criar simetria, equilíbrio e harmonia nas composições. Além disso, no design de logotipos e na criação de padrões geométricos usam os triângulos.
4. Construção de Estruturas
Os triângulos são essenciais na construção de estruturas como pontes e arranha-céus. O uso de triângulos, como em treliças, distribui as forças de maneira eficiente, permitindo que estruturas mais leves, mas extremamente resistentes, sejam construídas.
5. Física e Mecânica
Na física, especialmente na mecânica, os triângulos são usados em problemas de vetores e forças. A decomposição de forças em componentes é frequentemente realizada usando triângulos, sendo uma ferramenta crucial para o estudo de equações de movimento e equilíbrio.
6. Geometria Computacional e Gráficos 3D
Em computação gráfica, na construção de modelos 3D usam frequentemente os triângulos. Assim, as superfícies de objetos 3D são frequentemente representadas por malhas triangulares, facilitando o cálculo de luz, sombras e texturas nos gráficos de computadores.
7. Trânsito e Navegação
Sendo assim, na sinalização de trânsito, para indicar alertas e obstáculos usam os triângulos, como os triângulos vermelhos de emergência. em mapas de estradas para identificar rotas e distâncias usam também.
8. Desenvolvimento de Jogos e Simulações
Nos jogos de computador e simuladores, para representar formas e superfícies, especialmente quando a renderização de objetos em 3D é necessária usar os triângulos. Facilitando a modelagem e animação, cada objeto em 3D pode decompor em uma série de triângulos.
9. Astronomia
Ademais, na astronomia, para medir distâncias até estrelas ou planetas usam a técnica de triangulação. A partir de diferentes pontos de observação, usando o conceito de triangulação para determinar a localização de objetos celestes calculam as distâncias.
10. Construção de Telhados
O design de telhados de casas e edifícios muitas vezes envolve triângulos, especialmente em telhados com inclinação. O formato triangular ajuda a distribuir a carga da estrutura do telhado e permite que a água escorra adequadamente.
11. Fotografia e Vídeo
Além disso, na composição visual de fotografias e vídeos para criar uma sensação de equilíbrio e harmonia, frequentemente usam os triângulos. Para formar um triângulo, guiando o olhar do espectador, posicionam o conceito de “triângulo visual” é uma técnica em que os elementos de uma cena.
12. Medidas e Cálculos de Distâncias
Portanto, em técnicas de medição de distâncias inacessíveis usam os triângulos. Calcular a distância entre dois pontos que não podem medir diretamente é possível a partir de dois pontos de vista conhecidos e o uso de um triângulo.