O retângulo é uma figura geométrica que faz parte da família dos quadriláteros. Sendo caracterizado por ter quatro lados, sendo que os lados opostos são paralelos e possuem o mesmo comprimento. Além disso, os ângulos internos de um retângulo são sempre de 90 graus. Assim, essa forma é comum em várias situações do nosso dia a dia, desde o design de objetos até o planejamento de espaços. Desse modo, vamos entender melhor a definição, a utilidade do retângulo e apresentar exemplos e questões contextualizadas sobre o assunto.
O Retângulo no Cotidiano
Ademais, os retângulos estão presentes em muitas situações cotidianas, como em móveis, portas, janelas, telas de dispositivos eletrônicos e até na organização de terrenos. Sendo assim, a simplicidade dessa forma geométrica torna sua aplicação prática e eficiente. Vamos ver algumas dessas utilizações no cotidiano:
- Telhados e paredes de construções: Muitas casas e edifícios têm paredes e telhados em formato retangular.
- Móveis: Mesas, cadeiras, estantes e sofás muitas vezes seguem o formato retangular, facilitando o aproveitamento de espaço.
- Tecnologia: Telas de televisores, monitores e smartphones geralmente são retangulares, oferecendo uma visualização ideal de conteúdos como vídeos, imagens e textos.
- Impressão de documentos: Papéis de escritório, como o tamanho A4, são retangulares e amplamente usados para impressão e escrita.
Exemplos de Retângulo no Cotidiano
- Telha de telhado: Muitas telhas têm forma retangular para otimizar o encaixe e garantir um design eficiente para coberturas.
- Painéis solares: A maioria dos painéis solares são projetados em formato retangular para maximizar a captação de luz solar.
- Livros e cadernos: A grande maioria de livros e cadernos segue o formato retangular, o que facilita a impressão e o manuseio.
Agora que você já entende o conceito de retângulo e como ele está presente em nosso cotidiano, vamos resolver algumas questões contextualizadas sobre essa forma geométrica.
Questões Contextualizadas sobre o Retângulo com Resolução
1. Questão: Área de um Retângulo em um Terreno
Um terreno retangular possui comprimento de 20 metros e largura de 10 metros. Então qual é a área do terreno?
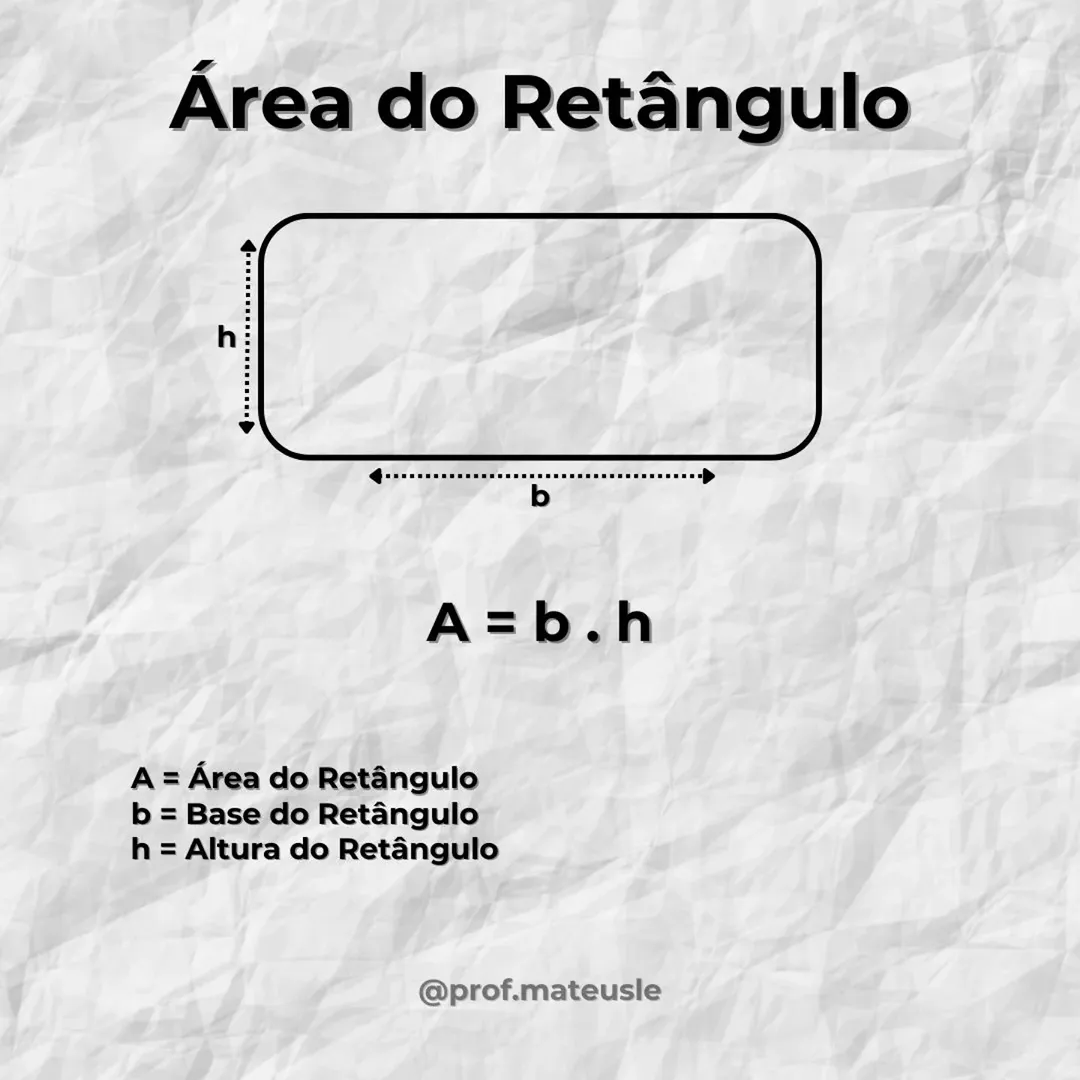
Resolução: A área de um retângulo é dada pela fórmula:
A = comprimento x largura
Substituindo os valores fornecidos:
A=20 m×10 m=200 m²
Resposta: A área do terreno é 200 metros quadrados.
2. Questão: Perímetro de uma Sala Retangular
Uma sala tem comprimento de 6 metros e largura de 4 metros. Qual é o perímetro da sala?
Resolução: O perímetro de um retângulo é dado pela fórmula:
P=2×(comprimento + largura)
Substituindo os valores fornecidos:
P=2×(6m+4m)=2×10m=20m
Resposta: O perímetro da sala é 20 metros.
3. Questão: Diagonal de um Retângulo em um Edifício
Em um edifício retangular, as dimensões do terreno são comprimento de 30 metros e largura de 40 metros. Então, qual é o comprimento da diagonal do terreno?
Resolução: A diagonal de um retângulo pode ser calculada usando o teorema de Pitágoras, onde a diagonal d é a hipotenusa de um triângulo retângulo formado pelo comprimento e a largura. Por fim, a fórmula é:
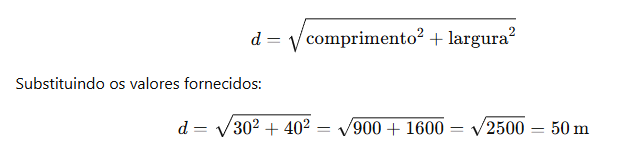
Resposta: O comprimento da diagonal do terreno é 50 metros.
4. Questão: Ajuste de Tela Retangular em um Dispositivo
Uma tela de smartphone possui as dimensões 15 cm de comprimento e 7 cm de largura. Qual é a área da tela?
Resolução: A área de um retângulo é dada pela fórmula:
A = comprimento × largura
Desse modo, substituindo os valores fornecidos: A = 15cm × 7cm = 105cm²
Resposta: A área da tela do smartphone resulta em 105 centímetros quadrados.
5. Questão: Proporção em uma Casa Retangular
Uma casa retangular tem comprimento de 12 metros e largura de 8 metros. Nesse sentido, qual é a razão entre o comprimento e a largura da casa?
Resolução: A razão entre o comprimento e a largura de um retângulo:

Resposta: A razão entre o comprimento e a largura da casa é 1,5.
Conclusão
Portanto, o retângulo é uma figura geométrica extremamente útil e presente em muitos aspectos do nosso dia a dia. Dessa maneira, desde o cálculo de áreas e perímetros em construções até o design de objetos tecnológicos, o retângulo desempenha um papel fundamental. Logo, compreender suas propriedades e saber aplicá-las em situações cotidianas é essencial, e as questões contextualizadas ajudam a consolidar esse aprendizado de forma prática e eficaz.