O retângulo é uma das figuras geométricas mais simples e ao mesmo tempo mais essenciais na matemática e no cotidiano. Com suas propriedades bem definidas, o retângulo aparece em diversas áreas, como arquitetura, design, física e até na natureza. Neste post, vamos explorar o conceito de retângulo, suas principais propriedades, formas de cálculo e as inúmeras aplicações dessa figura fundamental.
O Que é um Retângulo?
Um retângulo é um polígono de quatro lados, onde os ângulos internos são todos retos, ou seja, medem 90 graus. Ele é um tipo específico de paralelogramo, onde os lados opostos são de igual comprimento, mas, ao contrário do quadrado, seus lados adjacentes podem ter comprimentos diferentes.
Propriedades do Retângulo
O retângulo é uma figura com várias propriedades geométricas que o tornam único. Vamos destacar algumas das principais:
- Lados Opostos Iguais: Em um retângulo, os lados opostos têm o mesmo comprimento, o que o torna uma forma simétrica.
- Ângulos Retos: Todos os ângulos internos do retângulo são de 90 graus, o que garante a forma retangular.
- Diagonais Iguais: As diagonais de um retângulo têm o mesmo comprimento e se cortam no ponto médio da figura.
- Simetria: O retângulo possui duas linhas de simetria (uma horizontal e outra vertical), além de ser simétrico em torno do centro.
Como Calcular as Propriedades do Retângulo?
O retângulo possui fórmulas simples para o cálculo de sua área, perímetro e diagonal. Essas fórmulas são essenciais para resolver problemas geométricos e práticos relacionados à figura.
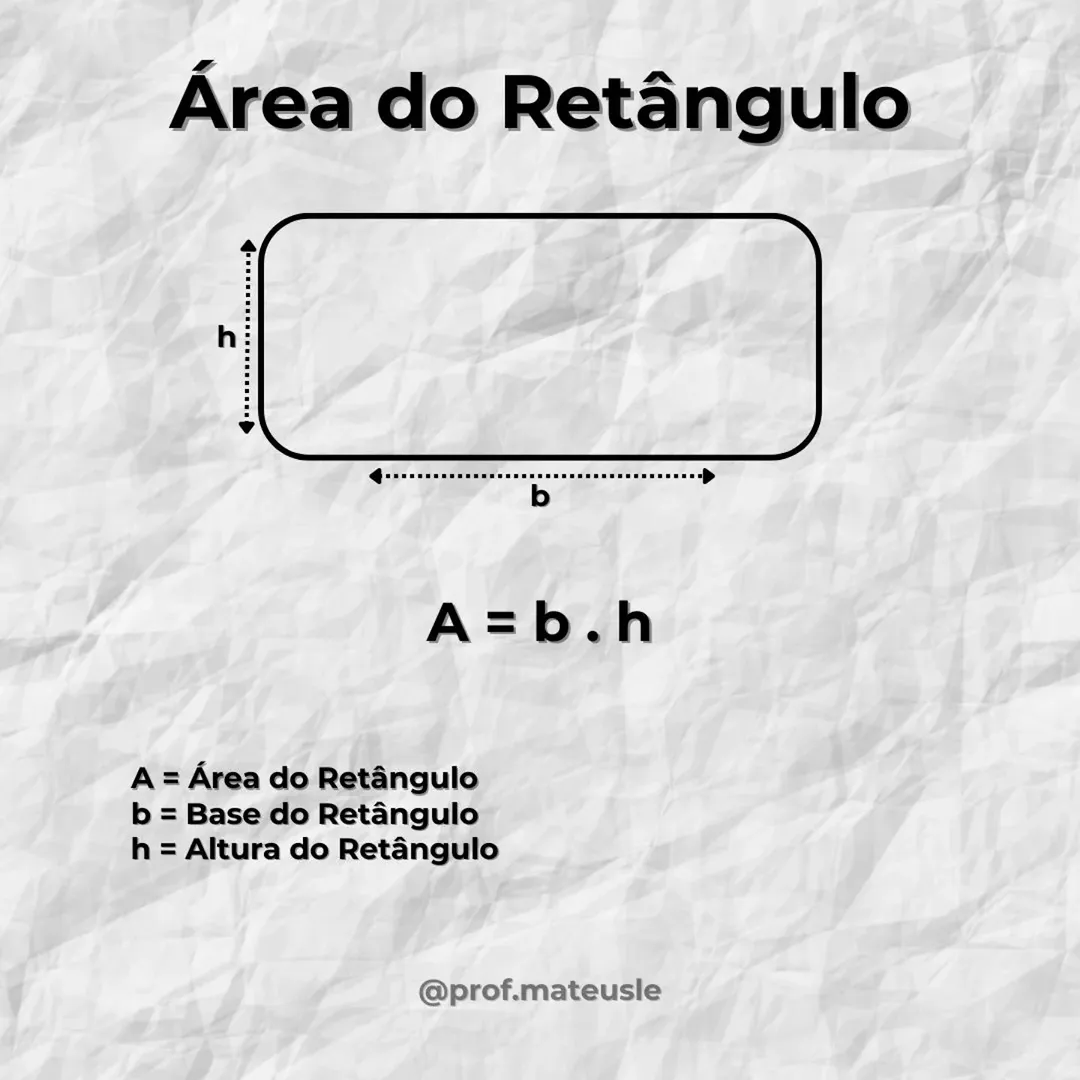
Área do Retângulo: A fórmula para calcular a área de um retângulo é dada por: A=L×A, no qual L é o comprimento e A é a largura do retângulo.
Perímetro do Retângulo: O perímetro do retângulo é a soma de todos os seus lados, sendo calculado pela fórmula: P=2×(L+A). Onde L é o comprimento e A é a largura.
Diagonal do Retângulo: A diagonal de um retângulo pode ser calculada utilizando o teorema de Pitágoras. Se L é o comprimento e A é a largura, a fórmula para a diagonal d é:
d = √L² + A²
Aplicações do Retângulo no Mundo Real
O retângulo é uma figura geométrica presente em muitas situações do nosso cotidiano. Sua simplicidade e versatilidade o tornam útil em diversas áreas:
- Arquitetura e Design de Interiores: O retângulo é amplamente utilizado no planejamento de espaços, como salas, edifícios, janelas e portas. Sua forma simples e a simetria tornam o retângulo ideal para criar ambientes funcionais e estéticos.
- Tecnologia e Design Gráfico: No design de interfaces de usuário e no design gráfico, o retângulo é frequentemente utilizado em elementos como botões, telas e banners. Sua clareza visual e alinhamento fácil com outras formas tornam-no indispensável.
- Física e Engenharia: O retângulo é utilizado na construção de estruturas, em projetos de engenharia e em cálculos relacionados a áreas de superfícies retangulares. Além disso, é fundamental em problemas de força e movimento, onde o retângulo é muitas vezes modelado como a base de um sistema de coordenadas.
- Matemática e Educação: O retângulo é uma das figuras geométricas mais simples a ser estudada, servindo como base para o entendimento de conceitos mais avançados na geometria e na álgebra, como a relação entre área e perímetro.
O Retângulo e Sua Relação com Outras Figuras Geométricas
O retângulo possui relações importantes com outras figuras geométricas, como o quadrado e o paralelogramo. Vamos ver algumas dessas relações:
- Quadrado: O quadrado é um caso específico de retângulo, onde todos os lados são iguais. Portanto, todo quadrado é um retângulo, mas nem todo retângulo é um quadrado.
- Paralelogramo: O retângulo é um tipo de paralelogramo, onde os ângulos internos são todos retos. Em um paralelogramo, os lados opostos são iguais, mas os ângulos nem sempre são retos, o que diferencia o retângulo.
Como o Retângulo é Usado em Problemas de Geometria?
Em muitos problemas de geometria, o retângulo aparece como uma base para cálculos de área e perímetro. Ele também é usado para resolver problemas de similaridade e proporcionalidade, especialmente quando lidamos com formas que envolvem a multiplicação ou divisão de lados. Além disso, sua relação com o teorema de Pitágoras, ao calcular a diagonal, torna o retângulo um elemento central em muitos tipos de cálculos geométricos.
Conclusão
O retângulo é uma das figuras geométricas mais importantes e amplamente utilizadas na matemática e em diversas áreas da vida cotidiana. Suas propriedades de simetria, ângulos retos e lados opostos iguais tornam o retângulo uma figura simples e ao mesmo tempo extremamente prática e versátil.
Compreender o retângulo é fundamental para o estudo da geometria e oferece uma base sólida para a resolução de muitos problemas matemáticos e práticos. Seja no design de um edifício, no cálculo de uma área ou na resolução de um problema físico, o retângulo é uma figura essencial para entender o mundo ao nosso redor.