As equações do 1º grau são um dos conceitos fundamentais na matemática e fazem parte do estudo da álgebra. Sendo assim, elas envolvem expressões algébricas em que a variável (geralmente representada por “x”) aparece apenas uma vez, e o seu expoente é 1. Desse modo, uma equação do 1º grau pode ser representada de forma geral como:
ax+b = 0
Onde:
- a e b são constantes (números conhecidos),
- x é a variável (o valor desconhecido a ser encontrado).
Definição Contextualizada:
Assim, em termos simples, uma equação do 1º grau representa um problema onde há uma relação linear entre a variável e os números conhecidos. Além disso, quando você resolve uma equação do 1º grau, então você está encontrando o valor da variável que torna a equação verdadeira.
Por exemplo, imagine que você tenha que resolver uma situação do cotidiano, como o seguinte:
Exemplo 1: Problema de Compras
Problema: João tem R$ 50,00 e quer comprar um brinquedo. O preço do brinquedo é de R$ 20,00, mas ele também precisa pagar uma taxa de R$ 5,00 de embalagem. Logo, qual o valor do brinquedo que João pode comprar, considerando que ele quer usar todo o seu dinheiro?
Equação: Vamos chamar o preço do brinquedo de “x”. A equação para resolver esse problema seria:
x+5=50
Aqui, x representa o preço do brinquedo, enquanto 5 corresponde à taxa de embalagem. Assim, a soma dessas duas quantias precisa ser igual aos R$ 50,00 que João tem disponível. Dessa forma, podemos estabelecer a seguinte equação para encontrar o valor do brinquedo:
x+5=50
x=50−5
x=45
João pode comprar um brinquedo que custa até R$ 45,00.
Exemplo 2: Problema de Distância
Problema: Um carro viaja a uma velocidade constante de 60 km/h. Se ele estiver viajando por “t” horas, qual será a distância percorrida?
Equação: A equação que representa o problema é:
60t=d
Onde d é a distância percorrida e t é o tempo em horas. Para encontrar a distância em função do tempo, basta substituir o valor de t. Por exemplo, se o carro viajou por 3 horas, temos:
60×3=d
d=180km
Portanto, a distância percorrida será de 180 km.
QUESTÕES CONTEXTUALIZADAS
1. Problema de Compras – Desconto
Enunciado: Você está em uma loja de roupas e encontra uma camiseta no valor de R$ 60,00. Nesse sentido, o vendedor oferece um desconto de R$ 10,00. Então quanto você pagará pela camiseta?
Equação:
x−10=60
Dessa forma, onde x é o valor que você pagará pela camiseta após o desconto.
Resolução:
x=60+10
x = 70
Você pagará R$ 70,00 pela camiseta.
2. Problema de Viagem – Velocidade e Tempo
Enunciado: Um trem viaja a uma velocidade constante de 80 km/h. Assim, quanto tempo ele levará para percorrer 320 km?
Equação:
80t=320
Onde t é o tempo em horas que o trem levará para percorrer 320 km.
Resolução:
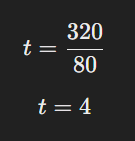
O trem levará 4 horas para percorrer 320 km.
3. Problema de Economia – Poupança
Enunciado: Maria quer economizar dinheiro para comprar um celular. Se ela economiza R$ 150,00 por mês e deseja juntar R$ 750,00. Desse modo, quantos meses ela precisará para alcançar esse valor?
Equação:
150m=750
m = 5
Maria precisará de 5 meses para juntar R$ 750,00.
4. Problema de Trabalho – Salário
Enunciado: Um trabalhador ganha R$ 2.500,00 por mês. Logo se ele receber um bônus de R$ 500,00, assim, qual será seu salário total?
Equação:
x+500=2500
Onde x é o salário sem o bônus.
Resolução:
x=2500−500
x=2000
O salário sem o bônus é R$ 2.000,00.
5. Problema de Distância – Corrida
Enunciado: Em uma corrida, um corredor percorre 12 km em 1,5 horas. Então qual é a sua velocidade média?
Equação:
v = 12/1,5
Onde v é a velocidade média em km/h.
Resolução:
v = 12/1,5
v = 8km/h
A velocidade média do corredor é 8km/h
Conclusão
Portanto, as equações do 1º grau são extremamente úteis para resolver uma ampla variedade de problemas, desde questões simples do dia a dia até problemas mais complexos em diferentes áreas, como física, economia e engenharia. Nesse contexto, ao entender o conceito e aprender a resolvê-las, você melhora sua capacidade de analisar e resolver problemas matemáticos de forma eficiente.