Você sabia que existe uma Fórmula de Euler para Poliedros simples, mas poderosa, que conecta os vértices, as arestas e as faces dos poliedros? A fórmula de Euler para poliedros é uma das mais importantes descobertas na geometria e se aplica a todos os poliedros convexos. Vamos entender como ela funciona e por que é essencial para a matemática!
O Que é a Fórmula de Euler?
Em primeiro lugar, a fórmula de Euler descreve uma relação fundamental entre o número de vértices (V), arestas (A) e faces (F) de um poliedro. A equação é:
V – A + F = 2
Portanto, isso significa que, para qualquer poliedro convexo, se você contar o número de vértices, subtrair o número de arestas e somar o número de faces, o resultado sempre será 2. Então, parece simples, mas essa relação é surpreendentemente poderosa e válida para uma vasta gama de formas geométricas!
Como Aplicar a Fórmula de Euler?
Vamos ver alguns exemplos para entender melhor como a fórmula funciona:
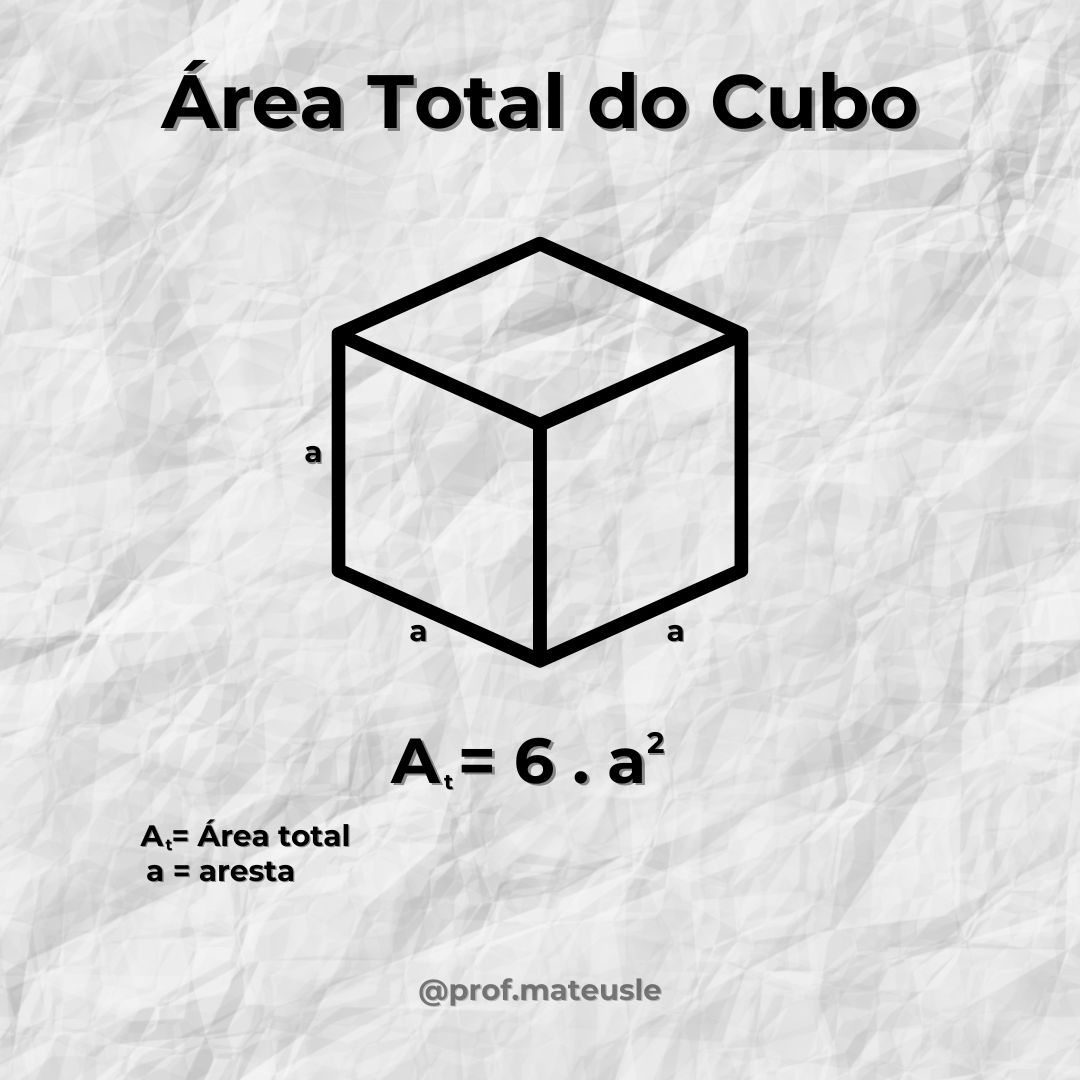
- Cubo: O cubo tem 8 vértices, 12 arestas e 6 faces. Vamos aplicar a fórmula: V – A + F = 8 – 12 + 6 = 2 Como esperado, o resultado é 2!
- Tetraedro: O tetraedro, que é o poliedro com o menor número de faces, tem 4 vértices, 6 arestas e 4 faces. Vamos calcular: V – A + F = 4 – 6 + 4 = 2 Mais uma vez, o resultado é 2!
Esses exemplos demonstram como a fórmula de Euler é universal, aplicando-se a diversas formas tridimensionais, e isso é apenas o começo. A beleza dessa fórmula é que ela pode ser usada para identificar características dos poliedros sem a necessidade de construí-los fisicamente.
Por Que a Fórmula de Euler é Importante?
A fórmula de Euler tem grande relevância tanto em matemática pura quanto aplicada. Ela ajuda a entender a topologia de objetos tridimensionais e também é fundamental em várias áreas como geometria computacional, modelagem 3D e até na construção de redes de computadores!
Conclusão
Portanto, a fórmula de Euler é um exemplo clássico de como a matemática pode nos proporcionar uma compreensão mais profunda do mundo ao nosso redor. Sendo assim, ao entender a relação entre vértices, arestas e faces de um poliedro, conseguimos não apenas resolver problemas geométricos, mas também explorar a beleza da simetria e da estrutura matemática.
Agora que você sabe como a fórmula funciona, que tal testar com outros poliedros e verificar se o resultado sempre será 2? A matemática nunca deixa de surpreender!