A equação do 1º grau é um dos conceitos fundamentais da álgebra e é usada para resolver uma ampla gama de problemas matemáticos. Nesse sentido, mesmo que muitas vezes não perceba, você já deve ter encontrado várias situações no seu cotidiano que podem ser resolvidas utilizando essa equação. Agora, neste post, vamos explicar o que é uma equação do 1º grau, como resolvê-la e mostrar exemplos práticos no dia a dia para você entender como aplicar esse conhecimento.
O que é uma Equação do 1º Grau?
Primeiramente, a equação do 1º grau é uma equação algébrica que tem a forma geral:
ax+b=0
Onde:
- a e b são números reais,
- x é a incógnita (o valor que queremos descobrir).
Esse tipo de equação envolve apenas potências de x elevadas a 1, ou seja, não existem quadrados, cubos ou outras potências de x. A solução de uma equação do 1º grau é sempre um valor numérico para x.
Como Resolver uma Equação do 1º Grau?
Resolver uma equação do 1º grau é simples e segue algumas etapas lógicas:
- Isolar a incógnita x: O objetivo é deixar x sozinho de um lado da equação.
- Realizar operações: Para isolar x, você pode somar, subtrair, multiplicar ou dividir ambos os lados da equação.
Vamos ver um exemplo simples:
Exemplo 1:
2x+5=15

Logo, a solução para a equação 2x+5=15 é x=5.
Exemplos Práticos do Dia a Dia
As equações do 1º grau aparecem frequentemente em diversas situações cotidianas, e entender como resolvê-las pode te ajudar a tomar decisões mais rápidas e precisas. Confira alguns exemplos práticos!
1. Divisão de Despesas em Grupo
Por certo, imagine que você e seus amigos querem dividir igualmente o custo de uma conta de restaurante. Se a conta total foi de R$ 120,00 e vocês são 4 pessoas, qual será o valor que cada um vai pagar?
Este é um exemplo simples de uma equação do 1º grau. A equação pode ser expressa como:
x × 4 = 120
Onde:
- x é o valor que cada pessoa vai pagar,
- 4 é o número de pessoas,
- 120 é o valor total da conta.
Resolvendo a equação:
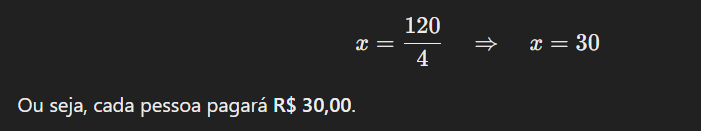
2. Planejamento de Economia
Além disso, suponha que você esteja economizando para comprar um celular. Você tem R$ 200,00 guardados e precisa de mais R$ 800,00 para alcançar o valor total do celular. Se você planeja economizar R$ 100,00 por mês, então quanto tempo levará para atingir o valor total?
A equação que descreve essa situação é:
200+100x=1000
Onde:
- 200 é o valor inicial que você já tem,
- x é o número de meses que você precisa economizar,
- 100 é o valor que você economiza por mês,
- 1000 é o valor total necessário para comprar o celular.
Resolvendo a equação:

Logo, você levará 8 meses para economizar o valor necessário para o celular.
3. Cálculo de Preço com Desconto
Imagine que você queira comprar um produto que custa R$ 250,00, mas há uma promoção de 20% de desconto. Quanto você pagará após o desconto?
Primeiro, calculamos o valor do desconto:
Desconto = 250 × 0,20 = 50
Agora, subtraímos o desconto do valor original:
Preço final = 250 − 50 = 200
Portanto, o valor final a ser pago é R$ 200,00.
Conclusão
Enfim, as equações do 1º grau estão presentes em diversos aspectos do nosso cotidiano, desde a divisão de despesas até o planejamento financeiro. Elas são uma ferramenta matemática simples, mas poderosa, que nos ajuda a resolver problemas práticos de forma rápida e eficiente.
Desse modo, agora que você entende como resolver uma equação do 1º grau e tem exemplos concretos de como aplicá-la no dia a dia, fica muito mais fácil perceber sua utilidade. Ou seja, para calcular valores, planejar economias ou dividir custos, essa habilidade matemática pode ser muito útil em várias situações!