Definição de Retângulo
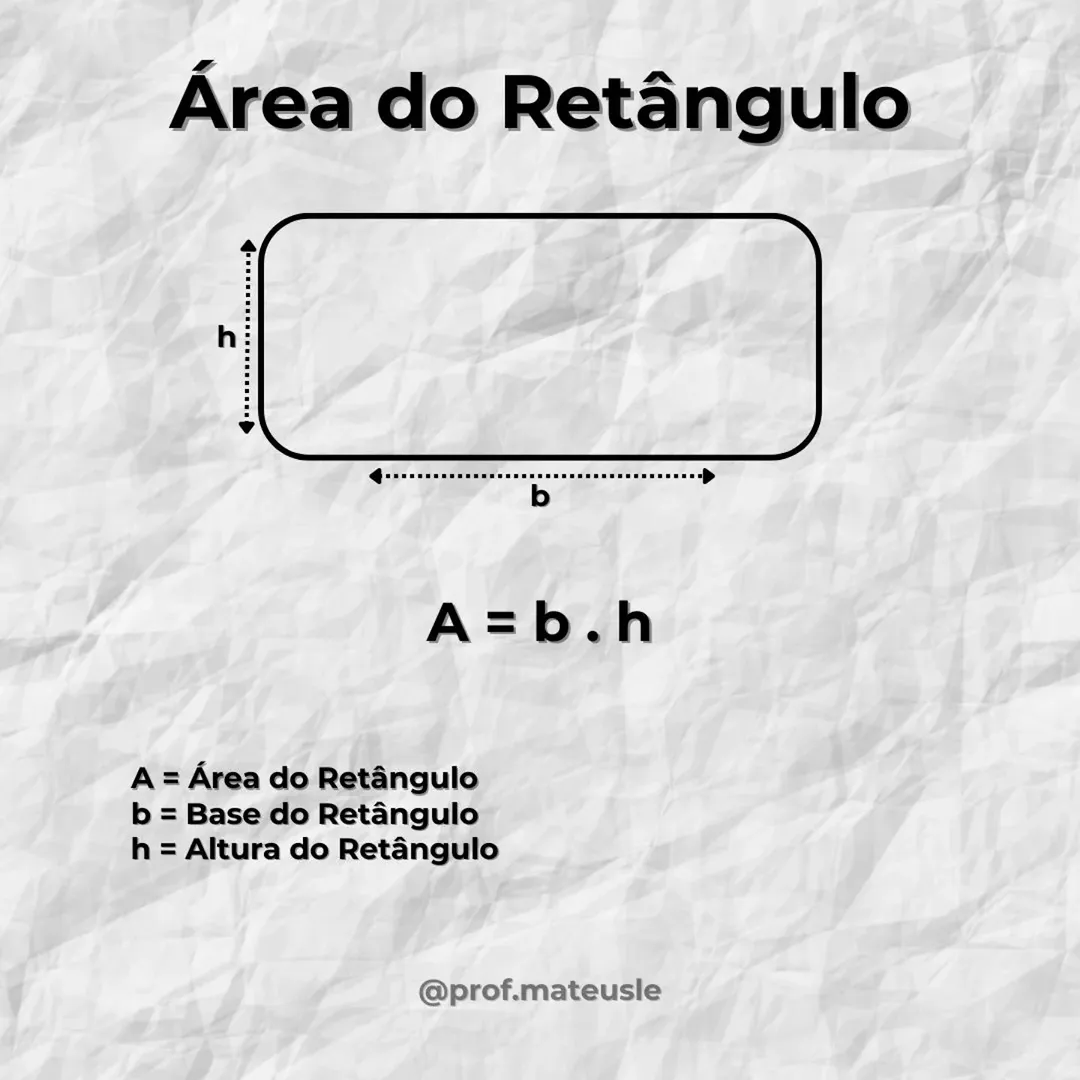
Primeiramente, um retângulo é uma figura geométrica plana pertencente à classe dos quadriláteros, que possui quatro lados, sendo dois pares de lados opostos e paralelos entre si. Além disso, todos os ângulos internos de um retângulo são retos, ou seja, possuem 90 graus. Logo, a fórmula para calcular a área e o perímetro de um retângulo é essencial em várias situações do cotidiano.
- Fórmula da área (A): A=base×altura
- Fórmula do perímetro (P): P=2×(base+altura)
Exemplos práticos
- Tela de um celular: A tela do seu celular é um retângulo, onde a base representa o comprimento e a altura é a largura. A área da tela é fundamental para determinar o tamanho da imagem ou do conteúdo exibido.
- Aparadores e mesas: Móveis em nossa casa, como mesas de jantar ou aparadores, muitas vezes têm o formato retangular. Isto é, a área da mesa ajuda a planejar o espaço disponível para colocar objetos.
- Rodovias: Algumas estradas e rodovias possuem seções retangulares, e conhecer a área e o perímetro pode ser útil para estimar o consumo de materiais para a construção de faixas e calçadas.
Cinco Questões Contextualizadas com Resolução Detalhada
1. Questão do Tamanho da Tela de um Celular
Enunciado: A tela de um celular tem 15 cm de comprimento e 7 cm de largura. Então qual é a área da tela?
Resolução:
Sabemos que a área de um retângulo é dada pela fórmula: A = base × altura
- Base = 15 cm
- Altura = 7 cm
Sendo assim, substituindo na fórmula: A = 15 cm × 7 cm = 105 cm²
Resposta: A área da tela do celular é 105 cm².
2. Questão sobre o Perímetro de uma Sala Retangular
Enunciado: Uma sala tem 6 metros de comprimento e 4 metros de largura. Assim, qual é o perímetro da sala?
Resolução:
A fórmula do perímetro de um retângulo é: P=2×(base+altura)
- Base = 6 m
- Altura = 4 m
Substituindo na fórmula: P = 2×(6 m+4 m) = 2×10 m = 20 m
Resposta: O perímetro da sala é 20 metros.
3. Questão sobre o Cálculo de Tecido para uma Cortina
Enunciado: Você quer comprar tecido para fazer uma cortina para uma janela retangular. Desse modo, a janela tem 2 metros de altura e 1,5 metros de largura. Então quantos metros quadrados de tecido você precisa comprar?
Resolução:
Ademais, como a janela é retangular, a área necessária de tecido será igual à área da janela. Então usamos a fórmula da área do retângulo: A = base × altura
- Base = 1,5 m
- Altura = 2 m
Substituindo na fórmula: A = 1,5 m × 2 m = 3 m²
Resposta: Você precisa comprar 3 metros quadrados de tecido.
4. Questão sobre a Área de um Quadro Retangular
Enunciado: Um quadro retangular tem 50 cm de comprimento e 40 cm de largura. Dessa forma, qual é a área do quadro?
Resolução:
A fórmula da área de um retângulo é a mesma: A = base × altura
- Base = 50 cm
- Altura = 40 cm
Posteriormente, vamos substituir na fórmula: A = 50 cm × 40 cm = 2000 cm²
Resposta: A área do quadro é 2000 cm² ou 0,2 m².
5. Questão sobre o Cálculo do Material para Piso de uma Sala Retangular
Enunciado: Você está renovando o piso de uma sala retangular que possui 8 metros de comprimento e 5 metros de largura. Quantos metros quadrados de piso você precisará comprar?
Resolução:
Para calcular a quantidade de material necessário, devemos calcular a área da sala, que é um retângulo. Usamos a fórmula da área do retângulo: A = base × altura
- Base = 8 m
- Altura = 5 m
Substituindo na fórmula: A = 8 m × 5 m = 40 m²
Resposta: Você precisará comprar 40 metros quadrados de piso.
Enfim, esses exemplos ilustram como o retângulo está presente no dia a dia e como suas propriedades podem ser aplicadas para resolver problemas práticos de maneira simples e eficiente.