O cubo é uma figura tridimensional bastante comum, mas entender as Questões Fundamentais sobre a Área Total do Cubo é essencial para vários contextos, tanto acadêmicos quanto práticos. Agora, neste post, vamos explorar a definição da área total do cubo, mostrar como ela aparece no nosso dia a dia e resolver cinco questões para consolidar o entendimento do tema.
O que é a Área Total do Cubo?
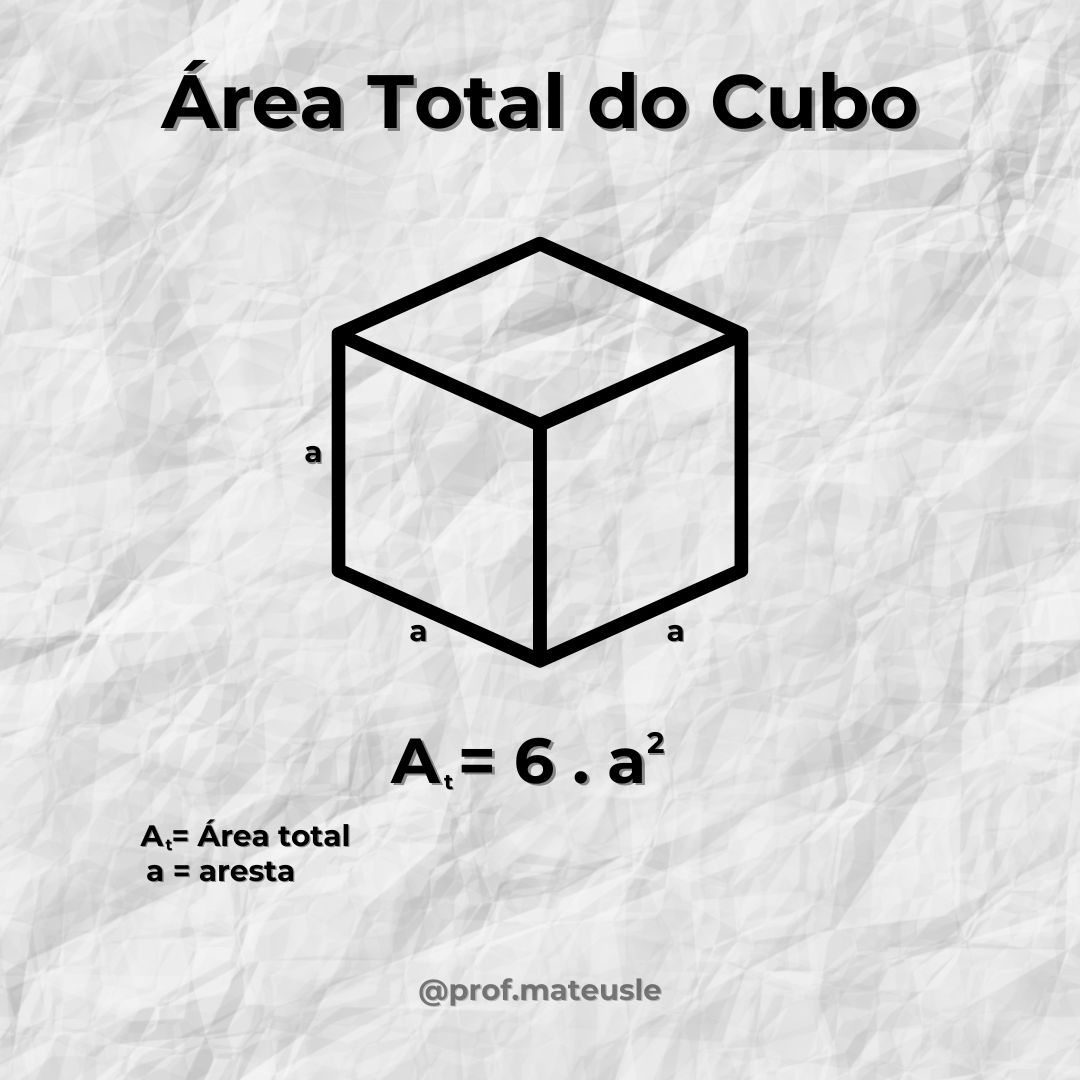
A área total do cubo é a soma das áreas das suas seis faces quadradas. Assim, como todas as faces de um cubo são quadradas e congruentes (têm a mesma medida), calcular sua área total é simples:
- Fórmula: Atotal=6×a²
- Onde:
- a é o comprimento da aresta do cubo.
Exemplos Práticos no Cotidiano
Primordialmente, o cubo está presente em muitos objetos do nosso dia a dia. Desse modo, vamos ver alguns exemplos:
Caixas de papelão: Muitas caixas de produtos, como brinquedos, alimentos ou eletrônicos, podem ter a forma de cubos. Dessa maneira, sabemos que a área total dessas caixas é a soma das áreas das seis faces, o que é útil quando se calcula a quantidade de material necessário para fabricá-las.
Cubo mágico: Também, o famoso brinquedo “Cubo Mágico” tem a forma de um cubo. Se quisermos saber a quantidade de tinta necessária para pintar todas as faces do cubo, podemos calcular a área total para determinar a cobertura necessária.
Blocos de construção (como Lego): Ademais, muitos brinquedos, como os blocos de Lego, têm a forma de cubo. O conhecimento da área total pode ser útil, por exemplo, em um projeto que envolva cobrir esses blocos com algum material.
QUESTÕES DA ÁREA TOTAL DO CUBO
Primeiramente, aqui estão cinco questões para entender de forma prática como calcular a área total do cubo, com resolução passo a passo.
Questão 1: Calcule a área total de um cubo cujo lado mede 4 cm.
Passo 1: A fórmula da área total do cubo é Atotal=6×a².
Passo 2: Substitua o valor de a (onde a=4cm).
Resposta: A área total do cubo é 96 cm².
Atotal=6×4²= 6 x 16 = 96 cm².
- Resposta: A área total do cubo é 96 cm².
QUESTÕES APLICADA NO COTIDIANO
Questão 2: Se a área total de um cubo é 150 cm², qual é o comprimento de sua aresta?
- Passo 1: Sabemos que a fórmula da área total é Atotal=6×a²
- Passo 2: Substituímos a área total (150 cm²) na fórmula. 150=6×a²
- Passo 3: Divida ambos os lados por 6.
a² = 150/6 = 25
Passo 4: Tire a raiz quadrada de 25 para encontrar a.
a = √25 = 5 cm
Resposta: O comprimento da aresta é 5 cm.
Questão 3: Um cubo tem a área total de 216 cm². Qual é o volume do cubo?
Passo 1: Sabemos que a fórmula da área total é Atotal=6×a².
Assim, usa-se a área total dada para encontrar a.
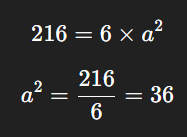
Passo 3: Tire a raiz quadrada de 36.
a = 6 cm
Passo 4: Agora que sabemos o comprimento da aresta, podemos calcular o volume do cubo, que é dado por V=a³
V = 6³ = 6 x 6 x 6 = 216 cm³
Resposta: Logo, o volume do cubo é 216 cm³.
Questão 4: Se o comprimento da aresta de um cubo é duplicado, então como a área total e o volume se alteram?
- Passo 1: Se o comprimento da aresta for duplicado, então o novo comprimento será 2a.
- Passo 2: A área total será dada por Atotal=6×(2a)²

- Ou seja, o volume será oitenta vezes maior.
- Resposta: Se o comprimento da aresta for duplicado, a área total será 4 vezes maior e o volume será 8 vezes maior.
Questão 5: Qual a área total de um cubo cuja aresta é 10 metros?
- Passo 1: A fórmula da área total é Atotal=6×a²
- Passo 2: Substitua a=10 metros.
Atotal=6×10²=6×100=600m²
- Resposta: A área total do cubo é 600 m².
Conclusão
Portanto, a área total do cubo é um conceito simples, mas muito útil para entender a geometria tridimensional. Sendo assim, com a fórmula Atotal=6×a², podemos resolver diversos problemas envolvendo cubos, seja no cálculo de área de embalagens, na indústria, ou até em projetos de construção. Além disso, vimos que a área total é uma base para entender outras propriedades do cubo, como seu volume.