O volume de um cilindro é uma medida fundamental em geometria, que nos ajuda a entender o espaço ocupado por esse sólido. Como um cilindro é uma figura tridimensional, calcular seu volume é essencial para diversas áreas, como engenharia, arquitetura e até mesmo na vida cotidiana, como no cálculo da capacidade de um recipiente cilíndrico.
Definição do Volume do Cilindro
Calcula-se o volume de um cilindro utilizando a fórmula:

A fórmula deriva do fato de que o volume de um cilindro equivale à área da base multiplicada pela altura.
Exemplo Prático
Vamos calcular o volume de um cilindro com um raio de 5 cm e altura de 10 cm.
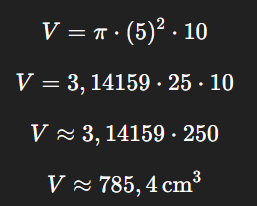
Portanto, o volume do cilindro é aproximadamente 785,4 cm³.
Agora, calcular o volume de um cilindro não se limita ao campo acadêmico. Sendo assim, na vida cotidiana, frequentemente lidamos com problemas práticos que envolvem esse cálculo. Dessa forma, desde o dimensionamento de recipientes até a análise de objetos cilíndricos, as situações em que aplicamos o volume de cilindros são muitas. A seguir, vamos explorar cinco questões cotidianas sobre o volume do cilindro, com exemplos práticos e resolução detalhada.
1. O que acontece com o volume do cilindro se a altura for dobrada?
Se a altura de um cilindro dobra, o volume também dobra, pois o volume é diretamente proporcional à altura.
Exemplo: Se um cilindro tem altura de 5 cm e raio de 3 cm, seu volume é: V=π⋅3²⋅5=141,37cm³
Se a altura dobra para 10 cm: V=π⋅(3)²⋅10=282,74cm³
Ou seja, o volume dobrou porque a altura dobrou.
2. Como calcular a quantidade de tinta necessária para pintar um cilindro?
Se você precisa calcular a quantidade de tinta para cobrir a superfície de um cilindro (como um tubo ou um pote), é necessário conhecer o volume da área a ser pintada, que está relacionada à área lateral do cilindro.
Exemplo: Considere um cilindro de altura 10 cm e raio 4 cm. Se você quiser cobrir a lateral do cilindro, a fórmula da área lateral é: A=2πrh
A=2π⋅4⋅10=251,33cm²
Portanto, para cobrir a lateral do cilindro, você precisaria de 251,33 cm² de tinta. Se a cobertura for para as extremidades também, calcule a área da base (2 vezes, pois o cilindro tem duas bases) e adicione ao resultado.
3. Quantos litros de gasolina cabem em um tanque cilíndrico de carro?
O tanque de um carro tem geralmente a forma de cilindro, e é muito importante saber a capacidade para garantir a quantidade de combustível necessária.
Exemplo: Suponha que o tanque tenha raio de 25 cm e altura de 70 cm. Para calcular o volume em litros (sabendo que 1 litro = 1000 cm³):
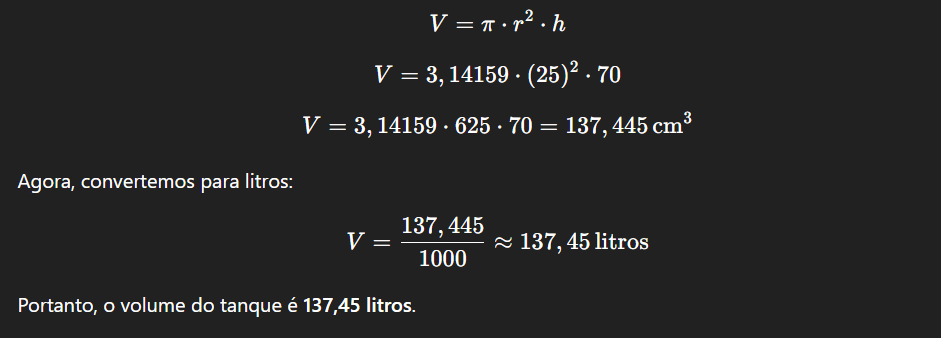
Portanto, o volume do tanque é 137,45 litros.
4. Como calcular o volume de um tubo de PVC para uso hidráulico?
Em projetos hidráulicos, como encanamentos e sistemas de irrigação, é importante conhecer o volume de tubos cilíndricos para determinar a quantidade de fluido que pode ser transportado.
Exemplo: Imagine que você tem um tubo de PVC com diâmetro de 10 cm e comprimento de 3 metros (300 cm). O raio será r=5 cm
Calculando o volume do tubo:

5. Como calcular a quantidade de concreto necessário para um pilar cilíndrico?
Em construção civil, pilares com formato cilíndrico são comuns. Para calcular a quantidade de concreto necessária para preencher o pilar, você precisa determinar o volume do cilindro.
Exemplo: Suponha que um pilar tenha raio de 30 cm e altura de 3 metros (300 cm). O volume do pilar será:

Conclusão
Enfim, esses exemplos demonstram como o cálculo do volume do cilindro é aplicado em situações cotidianas, como medir a capacidade de um tanque, calcular a quantidade de tinta necessária ou até mesmo estimar a quantidade de concreto para construção. Por conseguinte, com esses cálculos simples, é possível resolver problemas práticos no dia a dia, garantindo precisão e eficiência nas tarefas que envolvem cilindros.